Algebra Made Easy

Introduction

One of the key goals of any algebra course is to develop students’ algebraic problem-solving skills. This is especially important for 9th-grade students, as they are just beginning their high school journey and will encounter many new and challenging concepts in algebra.However, developing algebraic problem-solving skills is not always an easy task. Students may struggle with abstract concepts and find it challenging to apply algebraic concepts to real-world problems. Additionally, students may have difficulty with the language of algebra and the notation used to represent equations and expressions.Despite these challenges, it is essential to ensure that students have a strong foundation in algebraic problem-solving skills. These skills are not only important for success in future math courses but also for many careers that require analytical and problem-solving skills.In this report, we will explore various strategies and techniques that can be used to develop students’ algebraic problem-solving skills in 9th grade. By implementing these strategies, educators can help students overcome the challenges they may face and build a strong foundation for success in algebra and beyond.

Introduction to Algebraic Problem-Solving

Algebra is a branch of mathematics that uses letters and symbols to represent numbers and express relationships between them. Algebraic problem-solving involves using algebraic techniques to solve problems that involve variables and equations. These skills are essential in many fields, including science, engineering, and finance. In this section, we will introduce you to the basics of algebraic problem-solving and help you develop the skills needed to solve problems using algebra.

To begin with, it is essential to understand the basic algebraic operations, including addition, subtraction, multiplication, and division. These operations are used to manipulate algebraic expressions and equations, and they follow the same rules as arithmetic operations. For example, the commutative property of addition states that changing the order of the terms in an addition expression does not change its value. Therefore, 2 + 3 is the same as 3 + 2.

Another critical concept in algebraic problem-solving is the use of variables, which are letters or symbols that represent unknown or changing values. Variables are used to write equations and express relationships between quantities. For example, if we want to find the value of x in the equation 2x + 5 = 11, we need to use algebraic techniques to isolate x on one side of the equation.

Finally, it is essential to understand the order of operations, which is the sequence in which algebraic operations should be performed. The order of operations is as follows: parentheses, exponents, multiplication and division (performed from left to right), and addition and subtraction (performed from left to right). Following the order of operations is essential to ensure that the correct result is obtained.

By mastering these fundamental algebraic concepts, you will be able to approach algebraic problem-solving with confidence and develop the skills needed to solve complex problems. In the next section, we will explore how to use algebraic techniques to solve linear equations.

Simplifying Expressions with Variables

One of the fundamental skills in algebra is the ability to simplify expressions with variables. Simplifying an expression means to reduce it to its simplest form by combining like terms, removing parentheses, and performing any indicated operations. Here are the steps to simplify expressions with variables:

1. Combine like terms: Look for terms with the same variable raised to the same power and add or subtract them. For example, 3x + 2x can be simplified as 5x.
2. Remove parentheses: Use the distributive property to remove parentheses and simplify the expression. For example, 2(x + 3) can be simplified as 2x + 6.
3. Perform any indicated operations: If there are any remaining operations like multiplication, division, or exponents, perform them to simplify the expression further.

Let’s look at some examples:

1. Simplify the expression 4x + 2y – 3x – y.
2. First, combine like terms: 4x – 3x = x and 2y – y = y. Therefore, the simplified expression is x + y.
3. Simplify the expression 3(a + 2b) – 2(a – b).
4. Use the distributive property to remove parentheses: 3a + 6b – 2a + 2b. Then, combine like terms: 3a – 2a = a and 6b + 2b = 8b. Thus, the simplified expression is a + 8b.
5. Simplify the expression 2x^2 + 3x – 4x^2 + 5.
6. Combine like terms: 2x^2 – 4x^2 = -2x^2 and 3x = 3x. Then, add the constant term: -2x^2 + 3x + 5. The simplified expression is -2x^2 + 3x + 5.

Practice simplifying expressions with variables until you can do it quickly and accurately. This skill will be essential when solving more complex algebraic equations and problems.

Solving Linear Equations

Linear equations are equations that represent straight lines on a graph. They involve variables with a degree of one, which means they are raised to the power of one. Solving linear equations involves finding the value of the variable that makes the equation true.

There are several methods for solving linear equations, including:

• Using addition and subtraction to isolate the variable
• Using multiplication and division to isolate the variable
• Using the distributive property to simplify the equation before isolating the variable

Let’s look at an example:

3x + 5 = 11

To isolate the variable, we need to get it by itself on one side of the equation. We can start by subtracting 5 from both sides:

3x = 6

Next, we can divide both sides by 3:

x = 2

Therefore, the solution to the equation 3x + 5 = 11 is x = 2.

It’s important to always check your solution by plugging it back into the original equation to make sure it makes the equation true.

Practice solving linear equations with different methods to gain confidence in your algebraic problem-solving skills.

Graphing Linear Equations

Graphing linear equations is an essential skill in algebra that helps us visualize and understand relationships between variables. To graph a linear equation, we need to plot points that satisfy the equation and connect them with a straight line. In this section, we will learn how to graph linear equations using different methods.

Method 1: Using the Slope-Intercept Form

The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. To graph a linear equation in this form, we need to follow these steps:

1. Identify the slope (m) and the y-intercept (b) from the equation.
2. Plot the y-intercept (0, b) on the y-axis.
3. Use the slope to find another point on the line. To do this, we can use the rise-over-run method, which means we move up or down (rise) and right or left (run) from the y-intercept to get another point. For example, if the slope is 2/3, we can move up 2 units and right 3 units from the y-intercept to get another point.
4. Draw a straight line through the two points to represent the equation.

Let’s look at an example. Suppose we want to graph the equation y = 2x + 1. We can start by identifying the slope (m = 2) and the y-intercept (b = 1). Then, we plot the y-intercept (0, 1) on the y-axis and use the slope to find another point. Since the slope is 2, we can move up 2 units and right 1 unit from the y-intercept to get the point (1, 3). Finally, we draw a straight line through the two points as shown below:

Method 2: Using the Intercepts

Another method to graph a linear equation is to use its x- and y-intercepts. The x-intercept is the point where the line crosses the x-axis, and its y-coordinate is 0. The y-intercept is the point where the line crosses the y-axis, and its x-coordinate is 0. To graph a linear equation using its intercepts, we need to follow these steps:

1. Find the x- and y-intercepts of the equation by setting x = 0 and y = 0, respectively, and solving for the other variable.
2. Plot the x- and y-intercepts on the x- and y-axes, respectively.
3. Draw a straight line through the two points to represent the equation.

Let’s look at an example. Suppose we want to graph the equation 2x + 3y = 6. To find the x-intercept, we set y = 0 and solve for x:

2x + 3(0) = 6

2x = 6

x = 3

Therefore, the x-intercept is (3, 0). To find the y-intercept, we set x = 0 and solve for y:

2(0) + 3y = 6

y = 2

Therefore, the y-intercept is (0, 2). We can plot these two points and draw a straight line through them as shown below:

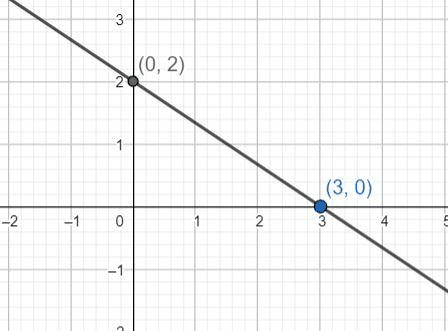
Practice graphing linear equations using both methods until you feel comfortable with them. Remember that graphing is a visual representation of an equation, and it can help you better understand the relationship between variables.

Word problems involving algebraic expressions and equations

Word problems are an essential part of algebra, as they allow us to apply algebraic concepts to real-life situations. In order to solve a word problem, we need to identify the unknown quantity and translate the information given in the problem into an algebraic expression or equation.

Let’s consider an example:

“A rectangle has a length that is 3 times its width. If the perimeter of the rectangle is 80 cm, what are the dimensions of the rectangle?”

We can start by defining the unknown quantities. Let x be the width of the rectangle. Then, the length of the rectangle is 3x. The perimeter of a rectangle is given by the formula: P = 2(l + w). Therefore, we can write an equation based on the information given in the problem:

2(3x + x) = 80

Simplifying the equation, we get:

8x = 80

Dividing by 8 on both sides, we get:

x = 10

Therefore, the width of the rectangle is 10 cm, and the length is 3 times that, or 30 cm.

It is important to check our answer by verifying that the perimeter of the rectangle is indeed 80 cm:

2(30 + 10) = 80

80 = 80

Our answer is correct.

Practice is essential to develop algebraic problem-solving skills. Try solving similar word problems on your own, and remember to define the unknown quantity, translate the information into an algebraic expression or equation, and simplify to solve for the unknown.

Achieving Success in 9th Grade Algebra Course

In conclusion, the 9th Grade Algebra Course is a crucial foundation for students pursuing higher education, especially in the fields of science, technology, engineering, and mathematics. This course provides students with essential algebraic problem-solving skills that are necessary for analyzing and solving real-world problems.

It is important for students to understand the significance of achieving success in this course, as it will pave the way for their future academic and career goals. By mastering the concepts covered in this course, students will develop the skills needed to advance to higher-level math courses, which are essential for many college majors and careers.

For those who may struggle with the course material, it is important to review this report and seek additional resources to help improve their algebraic problem-solving skills. There are many online courses available that can help students develop these skills and achieve success in their 9th Grade Algebra Course.

In conclusion, the 9th Grade Algebra Course is a fundamental course that sets the foundation for future academic and career success. It is crucial for students to embrace this course and strive to achieve mastery of the concepts covered.